五年级(上册)长方体和正方体的表面积(知识点+练习)

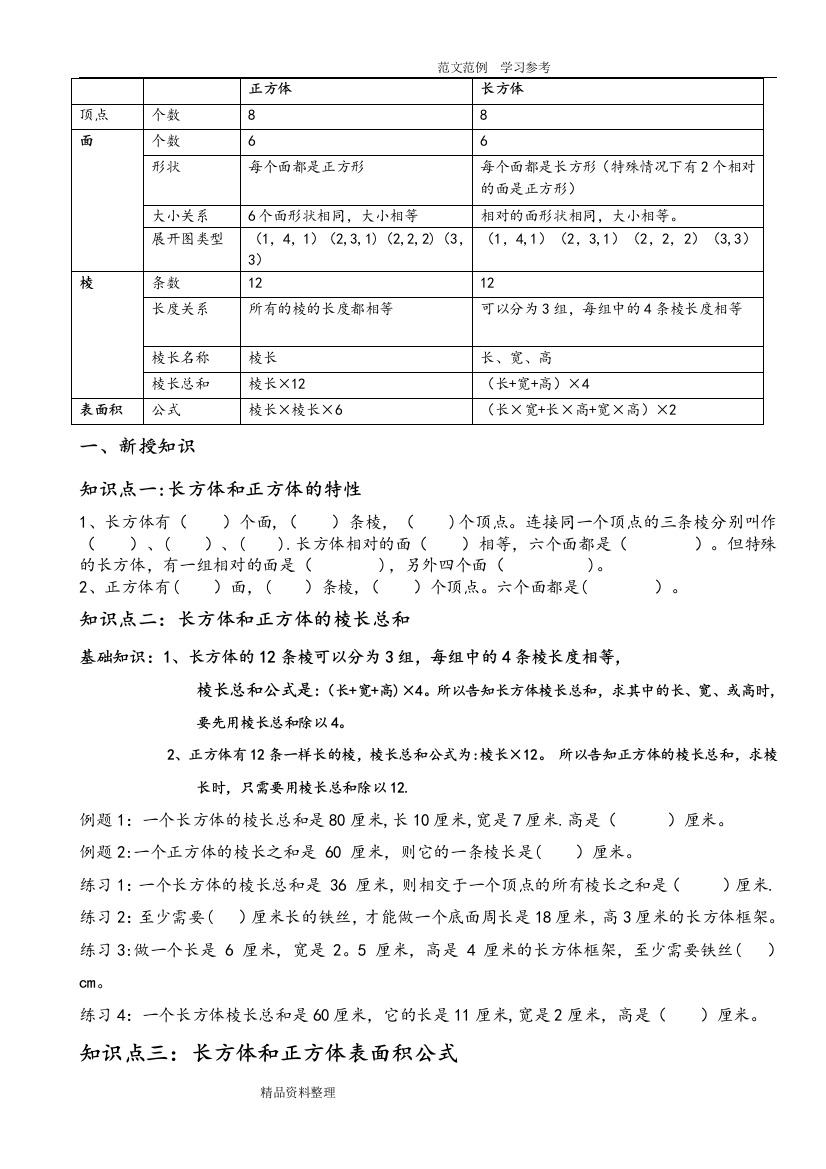
正方体长方体顶点个数88面个数66形状每个面都是正方形每个面都是长方形（特殊情况下有2个相对的面是正方形）大小关系6个面形状相同，大小相等相对的面形状相同，大小相等。展开图类型（1，4，1）（2,3,

范文范例学习参考 正方体 长方体 顶点 个数 8 8 面 个数 6 6 形状 每个面都是正方形 每个面都是长方形（特殊情况下有2个相对 的面是正方形） 大小关系 6个面形状相同，大小相等 相对的面形状相同，大小相等。 展开图类型 （1，4，1）（2,3,1)（2,2,2)（3，3） （1，4,1）（2，3,1）（2，2，2）（3,3） 棱 条数 12 12 长度关系 所有的棱的长度都相等 可以分为3组，每组中的4条棱长度相等 棱长名称 棱长 长、宽、高 棱长总和 棱长×12 （长+宽+高）×4 表面积 公式 棱长×棱长×6 （长×宽+长×高+宽×高）×2 一、 新授知识 知识点一:长方体和正方体的特性 1、 长方体有（）个面,（）条棱，（)个顶点。连接同一个顶点的三条棱分别叫作（）、 (）、().长方体相对的面（）相等，六个面都是（）。但特殊的长方体，有 一组相对的面是（)，另外四个面（)。 2、 正方体有(）面，(）条棱,（）个顶点。六个面都是(）。 知识点二：长方体和正方体的棱长总和 基础知识：1、长方体的12条棱可以分为3组，每组中的4条棱长度相等， （长+宽+高)×4。所以告知长方体棱长总和，求其中的长、宽、或高时， 棱长总和公式是: 要先用棱长总和除以4。 2、正方体有12条一样长的棱，棱长总和公式为:棱长×12。所以告知正方体 的棱长总和，求棱长时，只需要用棱长总和除以12. 例题1：一个长方体的棱长总和是80厘米,长10厘米,宽是7厘米.高是（）厘米。 例题2:一个正方体的棱长之和是60厘米，则它的一条棱长是(）厘米。 练习1：一个长方体的棱长总和是36厘米，则相交于一个顶点的所有棱长之和是（）厘米. 练习2：至少需要(）厘米长的铁丝，才能做一个底面周长是18厘米，高3厘米的长方体框架。 练习3:做一个长是6厘米，宽是2。5厘米，高是4厘米的长方体框架，至少需要铁丝(）cm。 练习4：一个长方体棱长总和是60厘米，它的长是11厘米,宽是2厘米，高是（）厘米。 知识点三：长方体和正方体表面积公式 基础知识：长方体的表面积=(长×宽+长×高+宽×高）×2 正方体的表面积=棱长×棱长×6 精品资料整理